打開 Google 地圖的街景功能,可能會發現一個明顯的現象:越靠近市中心,高樓大廈越是林立,一棟比一棟還要高聳。以台北市為例,車水馬龍與川流不息的人潮,常讓人感到壓迫與窒息。如果你是上班族,無論是租屋還是買房,在這樣的都市裡都是一場硬仗——高得驚人的房價,讓安居樂業成為一種奢侈的夢想。
不過,並不是所有都市都呈現這樣的樣貌。舉例來說,以美國的休士頓(Houston)或澳洲的布里斯本(Brisbane)為例,雖然也有明確的市中心,但都市整體較為分散,住宅區通常延伸至更寬廣的範圍。許多居民選擇居住在郊區,每天開車進城上班。在這些都市中,高樓林立的現象侷限於幾個小型商業區,更多的是低密度的獨棟住宅、草坪與車庫組成的社區景觀。
單一中心都市模型(Monocentric City Model)
都市空間的差異,其實正反映了不同國家、不同都市在「空間使用」、「交通方式」、「土地價格」以及「居民生活型態」上的根本差異。而這些看似毫無關聯的變數,其實可以用一套邏輯一致的理論來解釋:都市經濟學中經典的「單一中心都市模型」。此模型試圖回答幾個關鍵問題:為什麼市中心地價這麼貴?為什麼建物越靠近市中心越高?又為什麼郊區房子便宜、住戶空間變大、但人口密度反而下降?背後的關鍵在於——「通勤成本」與「土地競爭」。
當人們需要在「住得近一點、節省通勤時間」與「住得遠一點、獲得較大空間與較便宜租金」之間做選擇時,整座都市的空間分佈就自然呈現出一種規律:地價與房價由市中心往外遞減,而建物高度、人口密度也跟著改變。這種分佈不只出現在台北、東京或紐約,幾乎所有都市——只要有市中心、有通勤、有土地價格——都能在某種程度上觀察到這種現象。
模型假設
在討論之前,我們必須先瞭解單一中心都市模型如何描繪都市,以及都市中的「人」是如何與經濟體系互動。雖然模型會稍微簡化現實世界,但仍能捕捉部分的細節。
- 都市空間:模型假設都市裡的工作都在中心商業區(central business district, CBD),且將 CBD 視作一個點。從家裡到 CBD 的通勤路線是放射狀的(radial),並且假設可以沿著一條徑向道路直接通往 CBD,用 $x$ 表示距離 CBD 的遠近。
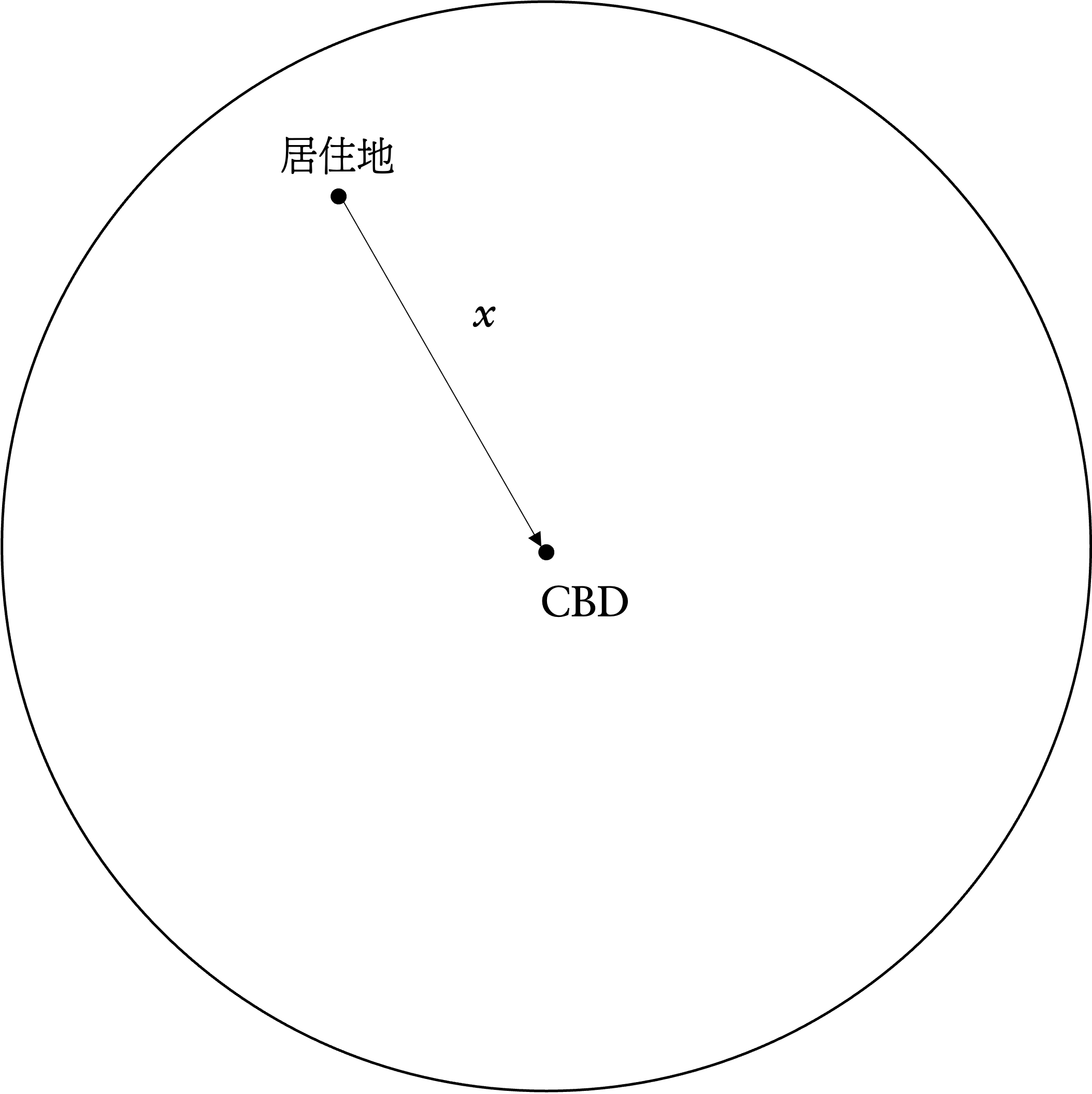
圖 1:都市中心商業區分析模型
家計單位:對家計單位而言,每個家庭都相同(identical),包含收入、偏好等都是一樣的,並計收入為 $y$,且都在 CBD 上班。家庭需要消費兩樣商品,一是住宅(housing),在此模型中設定為「住房空間的大小」,可以想像為坪數;二是其他除了房子以外的所有商品與服務所合成的其他一般商品[1]。
通勤成本:家計單位從家中至上班途中的通勤費用以 $t$ 表示,無論油錢、時間成本,全部均以金錢考量。因此若住在距離市中心 $x$ 的地方,通勤總成本就是 $t \times x$。因此在給定家計單位的收入為 $y$ 之下,扣除通勤費用後剩下 $y - tx$ 就是可支配於買房或一般商品的金額。
土地使用:模型僅關注住宅,因此假設工廠、商業用地等都集中在 CBD。每個地段上的建案由開發商(建商)興建並出租或出售給住戶,因此會同時考慮「家計單位的選擇」和「建商的利潤最大化」。
家計單位的選擇:為何越遠地價越低?
假設家計單位的效用函數為 $u = u(c, q)$,其中 $c$ 是消費的其他商品,$q$ 則是居住空間大小。家計單位所面臨的預算限制式可以表達為
$$
c + p(x) \cdot q = y - tx
$$
其中 $c$ 的價格被單位化為 1,而 $p(x)$ 代表離市中心 $x$ 地點的「每單位住房空間價格」,因此 $p(x)q$ 是家計單位在房租或房貸上的支出。因此,家計單位的效用極大化模型可以表達為
$$
\begin{aligned}
\max_{c, q}\;& u = u(c, q)\\
\text{s.t.}\;& c + p(x) \cdot q = y - tx
\end{aligned}
$$
另外,必須注意到,由於家計單位的效用都一樣,又可自由選擇居住地,因此若某地的「淨效用」較高,人們就會趨之若鶩搶著搬去該地住,直到房租或房價上漲到每個人的效用都持平為止。換句話說,在均衡時,不管住在市中心還是邊緣,都會得到一樣的效用水準,只是住得近的人少繳通勤費但要花更多租金;而住得遠的人少繳租金但多繳通勤費。最後結果是:$p(x)$ 必須隨著 $x$ 遞減,也就是距離市中心越遠,房價就應該要越便宜,才能夠補償每天高額的通勤成本。同時,由於較遠的房子較便宜,每個家計單位可以使用更大的空間,因此 $q(x)$ 隨著 $x$ 遞增。
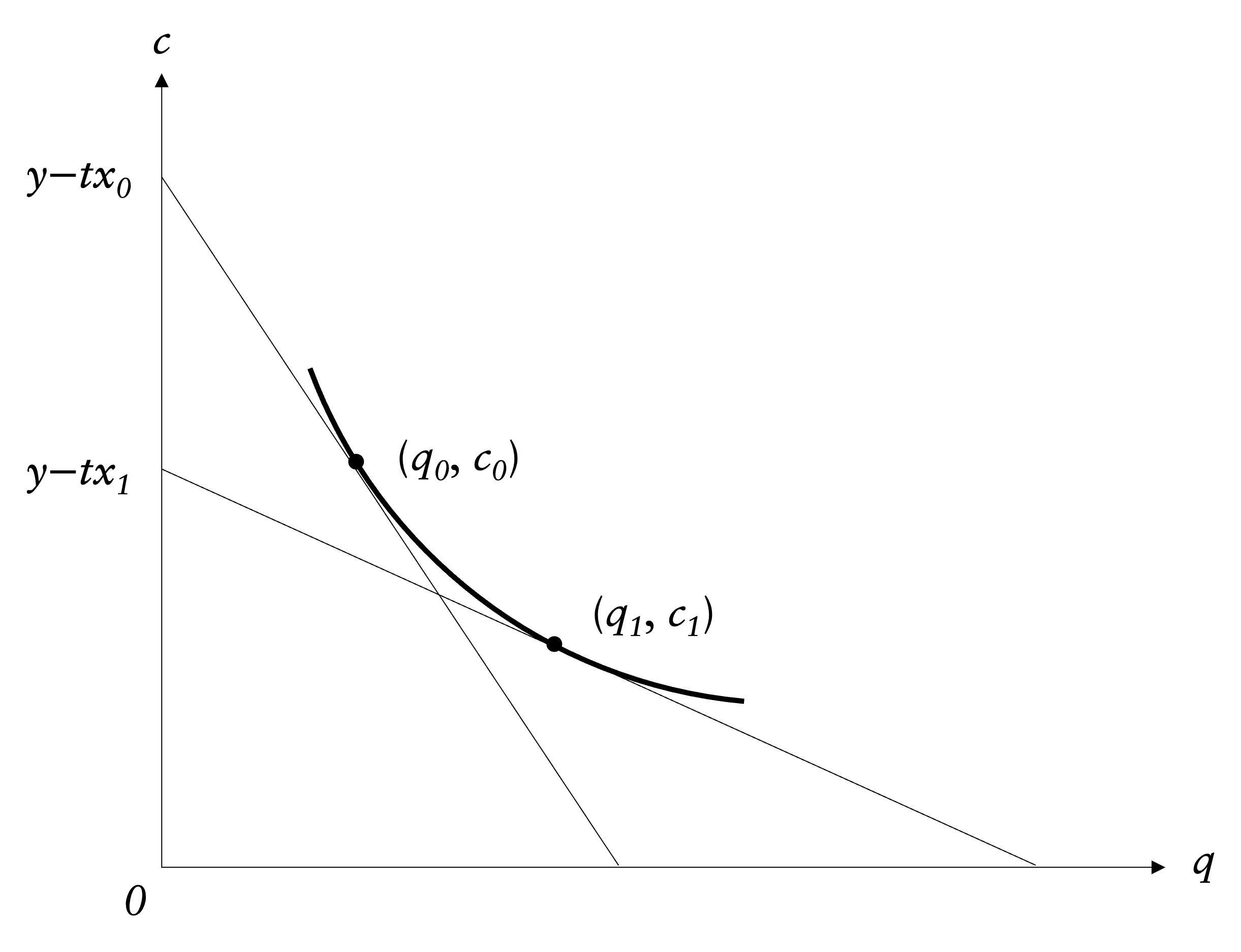
圖 2:效用函數與預算限制式
房價梯度
房價梯度(housing price gradient)的概念簡言之其實就是用來衡量房價如何隨著與市中心距離的增加而變化,特別是「變化的速率」是多少。房價梯度定義為
$$
\dfrac{\partial p(x)}{\partial x} = - \dfrac{t}{q(x)}
$$
先說結論:當距離市中心越遠,房價應該要降得越多,才能補償通勤費的增加。
證明
重述家計單位的效用極大化模型如下:
$$
\begin{aligned}
\max_{c, q}\;& u = u(c(x), q(x))\\
\text{s.t.}\;& c + p(x) \cdot q = y - tx
\end{aligned}
$$
因為模型假設所有家計單位都相同,收入也一樣,且可自由選擇住在任何距離市中心 $x$ 的地方,在均衡時,所有距離下的效用都相同。用數學的方法表達即是:
$$
u(c(x), q(x)) = \bar{u}, \quad \forall x \in \mathbb{R}
$$
其中 $\bar{u}$ 為固定的效用值,為一個常數(constant)。這行數學式的經濟意涵即是:如果住在比較遠的地方效用比較高,那大家就會搬去那裡,直到那裡的房價被推高;反之亦然。由於效用是固定的,因此可以對上式兩邊都對 $x$ 作微分,並同樣應用在預算限制式上,得到
$$
\begin{aligned}
\;&\dfrac{dc}{dx} + \dfrac{dp}{dx} \cdot q(x) + \dfrac{dq}{dx} \cdot p(x) = -t \\[5pt]
\;&\dfrac{du}{dx} = \dfrac{\partial u}{\partial c} \cdot \dfrac{dc}{dx} + \dfrac{\partial u}{dq} \cdot \dfrac{dq}{dx} = 0
\end{aligned}
$$
我們的目標是想要消去 $dc/dx$ 與 $dq/dx$,從而求出 $dp/dx$。由效用極大化條件可知
$$
\dfrac{MU_{c}}{MU_{q}} = \dfrac{\partial u/\partial c}{\partial u/\partial q} = \dfrac{p(x)}{1} = p(x)
$$
因此移項可得
$$
\dfrac{\partial u}{\partial c} = p(x) \cdot \dfrac{\partial u}{\partial q}
$$
將此式代入由效用函數微分後的結果,可得
$$
\begin{aligned}
\;&p(x) \cdot \dfrac{\partial u}{\partial q} \cdot \dfrac{dc}{dx} + \dfrac{\partial u}{dq} \cdot \dfrac{dq}{dx} = 0\\
\Rightarrow\;& \dfrac{\partial u}{\partial q} \left[p(x) \cdot \dfrac{dc}{dx} + \dfrac{dq}{dx}\right] = 0\\
\Rightarrow\;& \dfrac{dq}{dx} = -p(x) \cdot \dfrac{dc}{dx}
\end{aligned}
$$
代入此結果至預算限制式微分後的式子,得到
$$
\begin{aligned}
\;&\dfrac{dc}{dx} + \dfrac{dp}{dx} \cdot q(x) + \left[-p(x) \cdot \dfrac{dc}{dx}\right] \cdot p(x) = -t \\[5pt]
\Rightarrow\;&\dfrac{dc}{dx} + \dfrac{dp}{dx} \cdot q(x) + -p(x)^{2} \cdot \dfrac{dc}{dx} = -t \\[5pt]
\Rightarrow\;&\dfrac{dc}{dx}\left[1 - p(x)^{2}\right] + \dfrac{dp}{dx} \cdot q(x)= -t \\[5pt]
\Rightarrow\;&\dfrac{dp}{dx} \cdot q(x) = -t + \left[p(x)^{2} + 1\right] \cdot \dfrac{dc}{dx}\\[5pt]
\end{aligned}
$$
這時候如果 $dc/dx$ 很小,或效用是準線性(quasi-linear),可以忽略右邊後半,移項整理最終可得:
$$
\dfrac{\partial p(x)}{\partial x} = - \dfrac{t}{q(x)}
$$
- 假設 $dc/dx$ 很小的原因在於「住房空間」的選擇通常是主要考量,因為它直接受到房價和土地供給條件影響。相比之下,「一般消費品」的變動幅度通常相對小。尤其當都市裡生活用品價格固定(例如超市價格相同)時,即使住得遠一點、省下一些房租,多出來的錢也只是在消費品上略微增加,並不顯著改變效用水準。
- 如果是準線性效用函數,則效用函數可以寫成
$$
u(c, q) = c + v(q)
$$
如此設定之下,邊際效用對 $c$ 是常數,即 $\partial u/\partial c = 1$,$q$ 才是改變效用的主角。
□
建商的選擇:為何越近要蓋越高?
在此模型中,住宅的供給是由建商利用「土地」與「建築材料」共同生產出可居住的樓地面積($Q$),而此面積可以表示為以下的住宅生產函數:
$$
Q = H(N, l)
$$
其中 $N$ 是建材用量,$l$ 則為土地面積。此外,假設 $H$ 為固定規模報酬(constant return to scale, CRTS),亦即
$$
\lambda Q = H(\lambda N, \lambda l), \quad \lambda \in \mathbb{R}
$$
當建商想要將樓層越蓋越高時,邊際成本會隨之增加,可以想見,當大樓越高,就需要使用更多的鋼筋、水泥,從而將建築的結構加固。假設建商在某距離 $x$ 所支付的地租為 $r(x)$,購買建材的成本為 $i \times N$,其中 $i$ 為每單位建材價格,因此建商的成本函數可以表達為
$$
C(N, l) = iN + rl
$$
當建商在每個地點觀察到當地住宅單價 $p(x)$ 後,便會考量:
- 需要投入多少建材,以及使用多少土地(或購地多少),才能壓低成本生產最適量的住房空間,並以 $p(x)$ 出租/售。
- 在均衡時,競爭結果會導致建商的利潤為零(即建商僅賺取正常利潤),因為若某地利潤較高,其他建商都會在該處蓋房,直至地租 $r(x)$ 上漲,利潤被壓到 0 為止。
- 由於越靠近市中心的 $p(x)$ 越高,為了充分利用這塊昂貴土地,開發商就會投更多建材、蓋更高樓,以攤平土地成本。於是越靠近市中心,建築物越高,土地利用也越密集。
因此,地租會像房屋單價一樣呈現向外遞減的現象,而建材與土地的使用比例也隨著地價不同而改變:離市中心越近,土地貴、房價高,開發商就用更多建材,建出較高的樓。
人口密度:為何郊區人口較少?
誠如前述所言,離市中心越遠,房價越低,因此家計單位就會租賃更大間的房屋,代表空間被擠壓。雖然在市中心大樓很高,但是每戶住家空間 $q(x)$ 在市中心通常也較小,所以理論上整體「可住的人數」可能依舊密度很高。相反地,郊區的樓雖矮,可每戶空間大。因此討論人口密度時,需要綜合考慮「單位土地上的總樓地板面積」以及「每戶佔的單位面積」。將上述兩大因素結合,模型推導顯示,一般會得到「市中心人口密度高,往外距離增加而遞減」的結論。原因為
- 靠近市中心 → 雖然房子貴、房間小,但樓蓋得多且單位土地可容納較多戶;總體算下來人口密度往往高。
- 離市中心遠 → 雖然地便宜可蓋得寬,但每戶都想住更大空間,導致每單位土地能容納的戶數降低,總體密度相對小。
人口密度數學推導
用數學解釋如下:由於 $N(x)/l(x)$ 隨著 $x$ 遞減,言下之意就是隨著距離市中心越遠,土地面積越大、建築密度越低,郊區土地佔地寬裝,建物密度會較低。又前面已知 $q(x)$ 會隨 $x$ 遞增,這是因為遠離市中心的地價較便宜,住戶有更多資金來購買較大的住宅,所以隨著距離市中心越遠,每戶住宅的面積會增加。人口密度(population density)是指單位土地面積上的居民數量。在這個模型中,每戶家庭擁有 $k$ 人,所以人口密度 $D(x)$ 可以用下面的公式表示:
$$
D(x) = k \times \dfrac{H(N(x), l(x))}{q(x)} \times \dfrac{1}{l(x)}
$$
由於假設住房生產函數為固定規模報酬,因此上式可改寫為
$$
D(x) = k \times \dfrac{H(N(x)/l(x), 1)}{q(x)}
$$
綜上,因為 $N(x)/l(x)$ 隨著 $x$ 遞減,$q(x)$ 會隨 $x$ 遞增,因此 $D(x)$ 會隨著 $x$ 遞減。
都市邊界的決定因素
當都市發展到一定程度,土地價格將不再足以支撐都市的飛速發展,此時土地會轉作他用,例如農業生產、工廠擴建等。
- 都市的土地需求與供應之間會產生競爭:當都市的土地需求增大、市區土地價格上升,將會推動建商將原本的農業土地轉為都市建設用地。因此,農地收益提供了一個良好的外部選項,讓都市的人口得以「宣洩」。而正是因為如此,都市邊界正是都市土地和農業土地之間的分界線。
- 農地收益作為上限:如果土地價格高於農業收益,則都市會繼續擴張;若土地價格低於農業收益,都市擴展將會停止,並且農地將取而代之。
假設農地收益為 $r_{A}$,且地租曲線與農業收益的交點決定都市邊界 $\bar{x}$。此外,都市人口($L$)為外生給定,住房供應量必須滿足此人口需求,如此才能消除市場中的過剩需求或供應。假設所有都市居民都住在一個長度為 $[0, \bar{x}]$ 的區域內,則都市人口數為
$$
\int_{0}^{\bar{x}} D(x) dx = L
$$
若假設都市居民均住在一個半徑為 $\bar{x}$ 的圓形區域內,則
$$
\int_{0}^{\bar{x}} 2\pi x D(x) dx = L
$$
表示在圓形區域內,人口總數也是 $L$。不過在此模型中,因為已經假設都市是向外輻散的,因此第二個假設才比較符合模型設定。
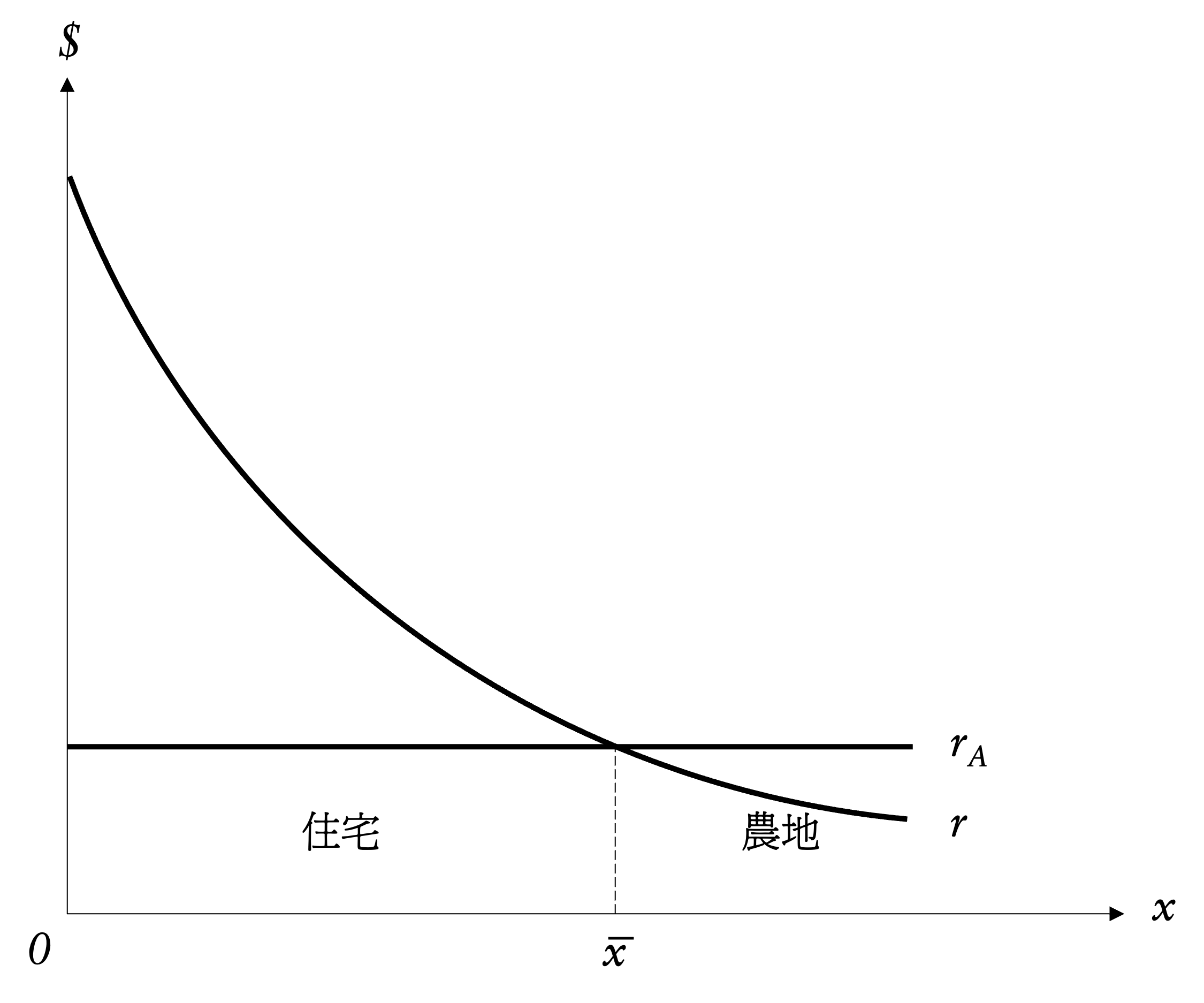
圖 3:都市邊界
都市結構與比較靜態
現在需要討論的是,如果某些外在條件改變,都市的結構會怎麼跟著改變?或者如何解釋不同都市之間的差異,或同一都市在不同情況下的變化。
人口數量增加
若有一座都市,人口從 $L_{0}$ 上升至 $L_{1}$。在變化初期,住房需求量必定上升,整體房價曲線必定上升。面臨租金/房價攀升,住戶只能選擇縮小居住面積。對於建商而言,因為地價上升,為了抵消成本,從而興建高樓,提供空間供給量。如此一來,同一個半徑下能夠住進更多人,進而將都市邊界向外推。因此當都市面臨人口數量上升,都市會變大、房價上升、市中心更密集、人口密度普遍上升、邊界向外擴張。
農地收益上升
如果郊外的農地或其他替代用途的收益增加,表示現在「搶」土地需要支付更高的地租。住宅用地一開始會相對短缺,房價因此攀升,因此住戶為了省錢,會減少居住空間。當建商看到地變貴了,就會將建物蓋的更加密集。整體人口仍可被容納,但因為市區地價也因競爭被推高,所以最終都市雖然能容納更多人,但邊界其實會「縮短」:地越來越貴,乾脆蓋高樓,往高處要空間,而不是往外擴張。
通勤成本改變
如果開車、搭車成本提高,住得遠就更不划算,因此更多人想往市中心靠近;市中心附近的房價因此上漲,而遠郊的房價反而下跌;整個都市人口分佈會往中心壓縮,邊界縮短。反之,若汽油成本、通勤成本下降(像高速公路、汽車普及),就會促進都市蔓延(urban sprawl):大家更願意住得遠,大房子、大院子,都市外圍越拓越大。
所得提高
原理和通勤成本幾乎相反。如果居民收入大幅提升,他們願意多花點通勤費,買更大房子或住得更舒適,並不一定要擠在市中心。因此都市整體會往外擴張,市中心的房價當然也會上漲,但人們可能選擇居住在更遠且更大的空間。
開放都市模型(Open City Model)
前面討論多半是假設「封閉都市」,人口數量固定。而若是「開放都市」,不同都市之間可以互相遷移,則:
更高收入的都市吸引更多移民,人口會持續擴張,直到當地房價、通勤成本等上升到讓新移民覺得「效用」跟別的都市差不多,才停止流入。
於是,有高所得機會的都市往往人口更集中、更大,房價也更貴。
修改後的單一中心都市模型
在單一中心都市模型中,家計單位被假設具有同質性,連收入都是相同的,但現實生活中,不同家計單位的收入可能不一,有高收入、小康家庭、中低收入戶以及低收入戶等。此外,就業分布也是原本模型未考量到的部分。房屋的耐久性(durability)也是另外一個影響都市結構的因素之一。因此在修改後的單一中心都市模型中,在假設其他條件不變的情況下(ceteris paribus),逐一放寬這些假設,討論這些改變對於都市空間結構的影響。
都市中的收入差異
假設都市內有兩個收入群體,分別為高收入群體(其收入記成 $y_{R}$)與低收入群體(其收入記成 $y_{P}$),且 $y_{R} > y_{P}$。可以觀察到,在美國,大多數的富人都會住在郊區,而窮人會願意著在市中心。不過這種反直覺的現象是否可以被模型合理解釋?答案是肯定的,原因是因為這兩個群體的住房需求不同所致:
- 低收入群體:由於低收入群體的收入相對較少,他們無法負擔市中心以外的高房價,因此他們通常選擇住在市中心。市中心的土地價格較便宜,且通勤成本較低,使得低收入群體能夠在相對較小的住房空間中承擔較低的租金或購房成本。
- 高收入群體:相對而言,高收入群體的收入較高,他們有更多的財務能力來選擇更大的住宅,通常會選擇住在郊區。雖然郊區的地價較低,但房屋空間較大,且雖然通勤成本較高,但高收入群體能夠承擔更高的通勤費用。在這樣的情況下,儘管通勤時間較長,但他們願意選擇遠離市中心的地方,享受更多的生活空間。
由上述可知,$q_{R} > q_{P}$,結合房價梯度,我們可以得出高收入群體的房價梯度較為平緩,原因基於:
$$
\dfrac{t}{q_{R}(x)} < \dfrac{t}{q_{P}(x)}
$$
從高收入群體的角度來看,房價梯度平緩代表的意義是,高收入群體願意承擔較高的通勤成本,加上高收入群體對居住條件要求高,對於房屋的需求呈現剛性。
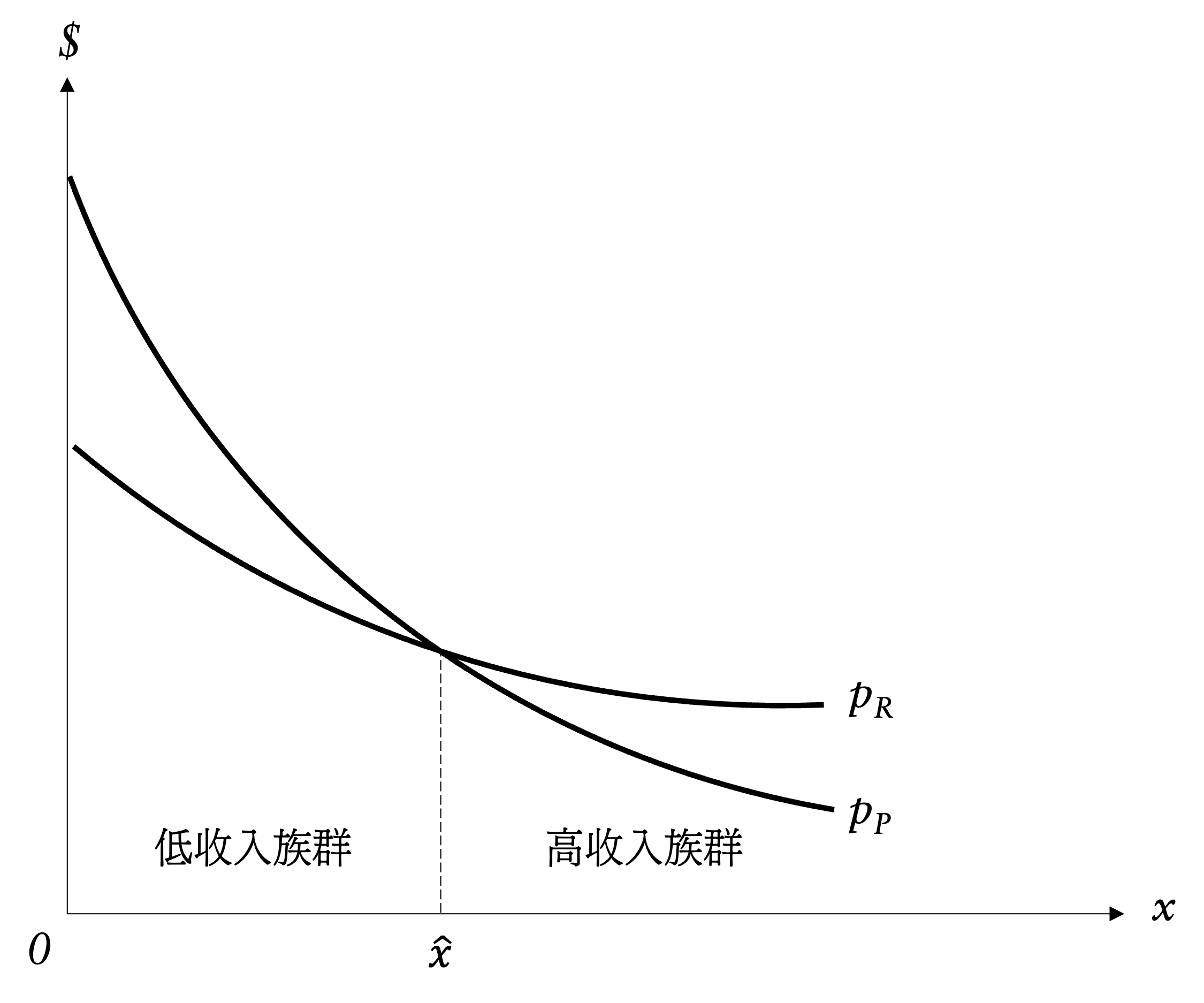
圖 4:高低收入群體房價梯度
注意到,兩群體的房價梯度曲線會在 $\hat{x}$ 交會一次,且只會交會一次。首先,該交會點代表在此點上兩群體的住房價格相同,即 $p_{R}(\hat{x}) = p_{P}(\hat{x})$,雖然高收入群體和低收入群體的房價相等,但由於高收入群體的每戶住房空間 $q_{R}(x)$ 較大,因此高收入群體的房價梯度在此交點之前會較為平緩。反之,低收入群體的房價梯度較陡。
至於是否合理,我們可以直接在模型中引入通勤成本與時間成本。假設個體一天的總時間可以被單位化為 1,令單位距離通勤時間(包含往返)為 $\delta$,因此工時為 $(1 - \delta x)$。高收入群體的薪水記成 $w_{R}$,低收入群體則為 $w_{P}$,且 $w_{R} > w_{P}$。此外,時間成本為每單位距離 $t$。因此,高收入群體住在距離市中心 $x$ 的地方時,其可支配所得即是總收入減去這些附加成本:
$$
(1 - \delta x)w_{R} - tx = w_{R} - \underbrace{(\delta w_{R} + t)}_{通勤成本}x
$$
因此高收入群體的通勤成本為 $m_{R} = \delta w_{R} + t$,同理可推得低收入群體的通勤成本為 $m_{P} = \delta w_{P} + t$。那麼,$m_{R}$ 與 $m_{P}$ 孰大孰小?其實這個答案無法確定,原因在於我們無法確定 $\delta w_{R}$ 與 $\delta w_{P}$ 的大小關係,個人觀點認為,高收入群體通常擁有較高的收入,他們對時間的價值會更加重視。在這種情況下,選擇私人轎車(例如 Uber)可以省去等候公共交通和在擁擠的交通中花費過多時間;即便這樣的選擇需要支付較高的成本,對他們來說,這筆額外費用是值得的,因為能夠節省時間和提升生活品質。
引入市中心外的就業機會
當都市中有更多的就業機會出現在市中心外,那麼都市結構會如何改變呢?可以考慮兩種情況,一是在都市中工作機會分佈在都市各地,而非集中於單一區域;二是假設都市內有次級商業區(secondary business district, SBD)。
在都市中廣泛分佈的工作
假設一名工人住在距離市中心 $x^{*}$ 的地方,在其通勤路上,某雇主提供一份距離市中心 $x^{**}$ 的工作。在此情況下,雇主為了吸引這名工人,會根據工人的通勤距離提供更高的薪水:
$$
y - tx^{\ast\ast} = y - t(x^{\ast} - x^{\ast\ast}) = y - tx^{\ast}
$$
工人如果接受這份工作,他的收入和生活成本會達到一個平衡點,即雇主會根據工人的通勤成本給予足夠的薪水,使工人對選擇接受這份工作與否無偏好。即使工作位置不在市中心,工人的可支配收入(即工資減去通勤成本)與選擇市中心工作相比,不會有太大區別。
次級商業區
假設都市中不只有市中心有工作機會,次級商業區也會提供,雖然薪資可能稍低、工作機會不多,或工作環境不同,但仍有人會選擇到此工作。如果市中心提供的薪水比次級商業區更高,那麼市中心的房價曲線會比次級商業區的曲線更高,表示越往市中心靠近,房價會更高;反之,離市中心越遠的地方,房價就會相對便宜。簡單來說,市中心工作提供更多收入,所以居住在市中心的人的收入也較高。
這裡就出現一個問題:如果次級商業區提供的工作比較少,或薪水不高,理論上應該會選擇住得比較近的地方工作,這樣可以減少通勤時間,省下更多時間和金錢。然而,現實中會出現一個問題:有些工人即使知道市中心工作的薪水更高,或者雖然次級商業區的工作薪水較低,他們還是會選擇長時間的通勤,這就叫做浪費通勤(wasteful commuting)。出現浪費通勤此一現象的原因眾說紛紜,但大致可以歸納為以下幾點:
- 對市中心的偏好: 有些人可能喜歡住在市中心,因為市中心有更多的便利設施(像是餐廳、商店、娛樂場所等)。即使工作不是在市中心,也會選擇住在市中心,接受更長的通勤時間。這是因為市中心的生活設施比其他地方豐富,對這些人而言,這些設施是值得的。
- 多工/雙薪家庭: 有些家庭可能有兩個工作的人,當這些工人選擇居住的地方時,他們並不僅僅考慮自己的工作地點,還會考慮配偶的工作地點。例如,配偶的工作地點可能就在市中心附近,所以整個家庭會選擇住在市中心,而不考慮次級商業區的工作地點,這樣就會導致浪費通勤。
住房耐久性
在先前的模型中,假設都市的建築是一次性建立的,也就是所謂的「一次性」模型。換句話說,在之前的模型中,建築不會隨時間變化,只是單純的在某個時間點建立並持續使用,沒有考慮時間上的延續性和變化。但在現實中,建築是有耐久性的,建築會隨著時間的推移而改變或老化,最終可能會被重建或維修(如都更)。
假設都市不斷向外擴展,每年新增一個固定距離的區域,這些區域被稱為區塊(block)。每個區塊代表都市的一個擴展部分,並且隨著時間的推移,這些區塊會在都市發展中逐漸形成。例如在時間 $T=0$ 時,都市的第一個區塊(Block 0)開始建設。隨著時間的推移,每隔一定時間,會新增一個新的區塊,並且這些區塊的建築會逐漸老化。每個新建的區塊會在它建立時建造新建築,並且每個建築都會持有一段固定的時間,然後這些建築將被拆除並重新建造。
假設每棟建築的使用年限是 3 年,也就是說:
- 在 $T=0$ 時建造的建築會在 $T=3$ 時被拆除並重新建造。
- $T=1$ 時建造的建築會在 $T=4$ 時被拆除,以此類推。
如此往復,就形成了都市內不同建築的年齡結構。隨著時間推移,都市中的建築會不斷更替,這會影響都市的外觀、居住條件以及經濟結構。另外,我們仍須考慮建築的高度與年齡的影響:
- 距離效應:隨著都市的擴展,距離市中心越遠的地方,建築的高度可能越低。原因是隨著距離市中心的增加,土地價格會逐漸下降,因此新建的建築可能會更矮小。
- 年齡效應:新建的建築可能會更高,而舊建築則相對較矮,即隨著時間的推移,舊建築的高度會逐漸降低,而新建的建築則可能更加現代化,並且高度更高。
開發中國家的都市化過程
目前多數開發中國家都面臨農村移往都市人口流動現象,以中國為例,目前中國的都市化程度尚不及 60%,但是多數已開發國家至少都超過此數字。從農村移往都市的過程,會改變都市的結構,成為一個值得討論的議題。
農村-都市人口遷移
前面已經提過,在開放都市模型中,假設都市人口為 $L$,都市邊界($\bar{x}$) 會隨著 $L$ 而增加,因此可以將都市邊界表達為以下的關係:
$$
\bar{x} = \bar{x}(L)
$$
由於農村居民通常不需要通勤,因此他們的選擇是基於都市邊界上與都市居民的比較。主要因為他們面臨的住房價格是一樣的。這意味著農村居民的選擇不受內部都市區域的影響,而只是與住在都市邊緣的居民的經濟條件進行比較。假設農村居民可支配所得為 $y_{A}$,且 $y - t\bar{x}(L)$ 為都市居民的收入扣除交通成本後的可支配所得,則
- 若 $y - t\bar{x}(L) > y_{A}$,代表都市居民的所得高於農村居民的可支配收入,農村居民會選擇遷移到都市。這會導致都市的人口 $L$ 增加,更多的農村居民被吸引進城。
- 反之,若 $y - t\bar{x}(L) < y_{A}$,代表都市居民的可支配所得低於農村居民的可支配所得,部分都市居民可能會選擇遷移回農村,都市人口因而減少。
均衡狀態達成的條件是:當都市居民的可支配所得等於農村居民的可支配所得,人口遷移將停止。換句話說,當都市的收入足夠吸引農村居民,並且農村的收入不再高於都市居民的收入時,人口遷移會達到一個平衡狀態。因此可以得到以下結論:當農村居民收入比較低時,大規模往都市的人口遷移將會發生。
都市均衡與人口規模
假設每個都市的住宅大小和高度在各地點都是固定的,從而簡化模型,避免了不同地點的住宅高度變動。假設人口密度是固定的,表示為 $\theta$,並定義 $\mu = 1/\theta$ 為人均佔地面積。在這個模型中,都市的均衡是基於人口規模 $L$ 與都市邊界的關係。房屋供需均衡時會滿足
$$
\mu L = \pi \bar{x}^{2}
$$
在都市的均衡情況下,都市的土地使用量由以下公式決定:
$$
y - t\bar{x} = y_{A}
$$
代入房屋供需均衡的條件,可得
$$
y - t\sqrt{\dfrac{\mu L}{\pi}} = y_{A}
$$
- 當 $y$ 增加時,這表示都市居民的收入上升,那麼為了保持均衡,都市的總人口 $L$ 也會隨之增加。這是因為都市提供了更高的收入,吸引更多的農村居民遷入都市。
- 當 $t$ 減少時,交通成本降低,也會促使更多的人遷入都市,從而增加都市人口。
- 當 $y_{A}$ 減少時,即農村的收入減少時,農村居民的遷移到都市的動機增強,也會增加都市的人口規模。
Harris-Todaro 模型
儘管都市的失業率很高,為何農村居民會趨之若鶩搬遷至都市居住呢?
為了回答此問題,Harris-Todaro 模型給出「預期收入」的概念,而非僅僅仰賴現實的就業機會。對於一個來自農村的居民來說,決定是否遷入都市的關鍵因素不僅是都市的現有就業機會,而是他們根據都市的就業機會和農村的生活條件所預期的收入。假設都市有 $J$ 個工作機會,都市總人口為 $L$,但並非每個人都能成功找到工作,但為了方便起見,假設每個人都有相同的就業機會,找到工作的機率為 $J/L$。均衡條件為
$$
y \times \dfrac{J}{L} - t\sqrt{\dfrac{\mu L}{\pi}} = y_{A}
$$
其中 $y$ 為都市居民的平均所得,$y_{A}$ 為農村居民的所得。上式代表都市的預期收入(扣除交通成本)必須等於農村的收入,這樣才會達到平衡狀態。若都市的收入高於農村的收入,則農村居民會遷移到都市,增加都市的人口。當都市的工作機會增加,或交通成本減少,將使都市對農村居民的吸引力增強,從而導致更多的農村居民遷入都市。
- 1.直觀地可以想像到,模型的設定就是要儘量捕捉人類的生活習慣,至少需要一個地方居住,且需要食物來補充身體所需的能量。 ↩