日常生活中,我們可以觀察到城市與城市之間存在明顯的大小以及等級差異。以臺灣為例,儘管臺北在縣市層級上屬直轄市,聚集了各種高級的服務、大型商場與醫療資源;相較之下,其他小鎮、鄉村僅提供基本生活所需,並無眾多的設施。臺灣並非特例,世界各國均是如此。
- 為什麼城市間會有大小與距離的差異?
- 為什麼大城市比較少,小城市比較多?
- 如何安排城市的分佈,才能達到「成本最低」的社會最適狀態?
為了回答上述問題,德國地理學家 Walter Christaller 在 1933 年所著之《Die zentralen Orte in Süddeutschland》提出了中地理論(central place theory),經諸多經濟學家的發展,成為空間經濟學中的重要理論。
何謂中地理論?
Christaller 認為,在一片地形平坦、肥沃度一致、農夫平均分佈的平面上,城市會自然行程一個層級結構,而該平面稱為均質平面(homogeneous surface)。
中地:每個城市都有一個服務區域,城市為區域內的居民提供商品與服務,該城市就稱為中地。
商品有高低等級之分:像牙膏、肥皂這種需求高、成本低的商品,小城市就能提供;但像醫院、戲院、百貨公司這種需求少、成本高的服務,只有大城市有。
層級性原則(hierarchy principle):大城市一定會提供小城市有的所有商品,加上一些只有它才有的。
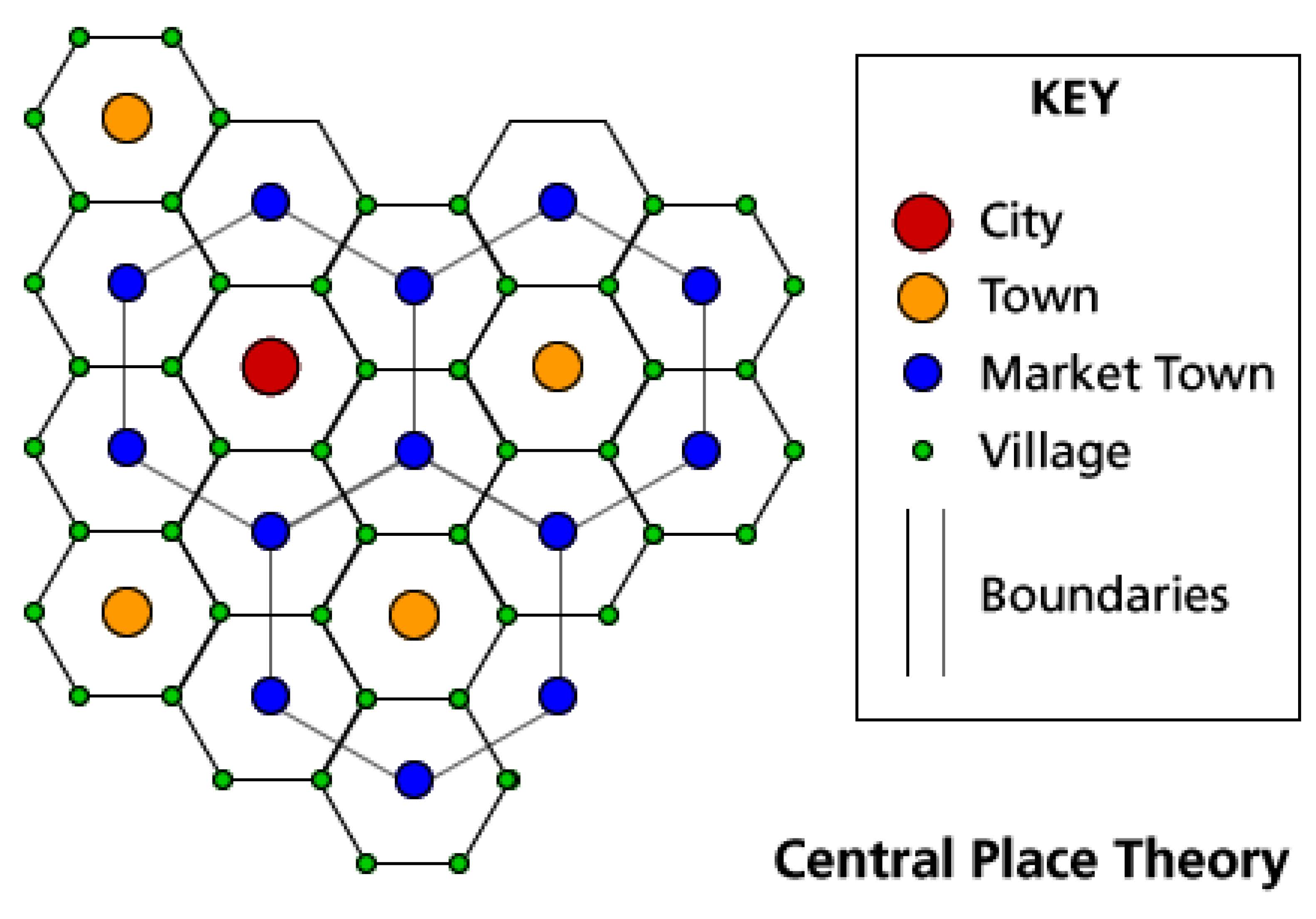
圖 1:中地示意圖[1]
例如小鎮上只能買到雜貨店或便利商店的東西,但你要買 IKEA 家具就得去大城市,這就是層級性。
現代中地理論
傳統的中央地理論雖然成功描繪出城市層級的圖像,卻缺乏足夠的數學基礎,難以被現代經濟學接受。因此,學者們開始嘗試用更嚴謹的模型來「形式化」這套理論,試圖解釋城市分布與規模差異的根本經濟邏輯。
首先,我們將探討一個經過簡化的現代中地理論模型。這個模型的目的是透過數學推導,說明城市的層級結構如何在「社會最適」(即整體成本最低)的條件下自然形成。這樣的層級不是被政府強制設計出來的,而是源自於規模經濟與運輸成本之間的權衡結果。
模型設定
為了簡化模型,假設整個空間是一條無限延長的直線,即整條實數線 $\mathbb{R}$,如此一來便可避免左右邊界造成不對稱的問題。沿著此線上,有無限多的消費者均勻分佈(uniformly distributed),每單位長度的密度設定為 $d$。
消費者需求
每個消費者對商品有固定需求。我們將商品視為一個區間 $[0, z_{1}]$ 上的連續點,也就是每個數字 $y \in [0, z_{1}]$ 均代表一種商品,越靠近 $z_{1}$ 等級越高。每人每天都需要一單位的每種商品,需求不受價格影響,即完全無彈性,且無論城市設在哪裡,總需求都是一樣的。
商品與生產成本
廠商生產每一種商品 $y$ 都需要支付一筆固定成本 $\phi(y)$,且商品等級越高,成本就越高,亦即 $\phi^{\prime}(y) > 0$,且如果不生產產品,則 $\phi(0) = 0$。邊際生產成本為常數 $c$,但後續分析會被忽略,因為對每個人而言是固定的,不影響最終決策。[2]既然生產過程中有固定成本,那麼該生產活動就會具有規模經濟(scale of economies),原因是因為規模經濟的定義是隨著產量增加,平均成本降低。[3]根據上面的假設,廠商生產 $q$ 單位的總成本為
$$
TC(q) = \phi(q) + c \cdot q
$$
則平均成本為
$$
AC (q) = \dfrac{\phi(q) + c \cdot q}{q}
$$
可以發現當 $q$ 越大,$\phi / q$ 越小,整體的平均成本就會越低。簡言之,只要有固定成本,只要生產越多單位,就越能平均分攤這筆固定開銷,平均成本就會下降,因此會產生規模經濟。另外,模型假設若商品要運送給消費者,每單位距離每單位商品的運費是常數 $t$。因此,距離越遠,成本就越高。
層級性原則
每個生產地點(即一個城市)如果要生產某個高等級商品 $z$,那麼它必須也生產所有比其低等級的商品 $y < z$[4]。此外,每個城市所提供的商品一定是從最基本的 0 開始,一直到某個等級 $z$ 為止,是一個連續區間 $[0, z]$,不會跳過任何商品。所以我們只要知道它能生產哪個「最頂」的商品 $z$,就知道它的整個商品清單是 $[0,z]$。如果一座城市最高能提供商品 5,那就代表它一定也有 0 至 4 號商品。我們就叫它一座「$z=5$ 的城市」,簡稱「5-city」。
圖 2:層級性原則[1]
如果城市如果要提供從 0 到 $z$ 的所有商品,那它要承擔的總固定成本(蓋工廠、設施)就是把每種商品的固定成本 $\phi(y)$ 從 0 加總到 $z$ 為止,即是
$$
\Phi(z) = \int_{0}^{z} \phi(y) dy
$$
另外,前面假設 $\phi(y)$ 是遞增的,代表越高階商品固定成本越高,根據微積分基本定理,可得到 $\Phi(z)$ 的一階與二階條件如下:
$$
\Phi^{\prime}(z) = \phi(z) > 0, \quad \Phi^{\prime\prime}(z) = \phi^{\prime}(z) > 0
$$
要成為「高階城市」成本很高,越高越貴,這就是現實中為什麼只有少數幾個大都市能提供最頂級的服務。
社會規劃者問題
根據前述討論,由於每個人消費相同的東西,消費量也一樣,因此模型可以忽略變動成本,僅考慮固定成本 $\Phi(z)$ 與運輸成本 $t$。現在要從「上帝視角」安排整個空間上的城市,這個社會規劃者負責決定每個城市的位置與距離,目標是讓所有消費者的平均成本最低。
由於消費者平均分佈在空間上,因此不管在哪一段距離,需求都是相同的,最有效率的安排方式就是把城市平均分配在空間上,這些城市都是最大城市,即生產所有商品 $z_{1}$ 的城市,稱為 $z_{1}$-city。現在要來計算兩個 $z_{1}$-city 中間那一段距離上,平均每個人為了拿到商品,要付出多少運費?假設兩座城市距離為 $\ell$,每個人都會去最近的城市購買商品,所以一個城市的服務半徑是 $\ell/2$。因為消費者平均分佈,密度為 $d$,每人運費距離 $x$ 乘上每公里成本 $t$,因此把 $0$ 到 $\ell/2$ 的所有運費加總就得到
$$
2d \int_{0}^{\ell/2} tx dx = \dfrac{dt\ell^{2}}{4}
$$
- 1.Hsu, W. T., Holmes, T. J., & Morgan, F. (2014). Optimal city hierarchy: A dynamic programming approach to central place theory. Journal of Economic Theory, 154, 245-273. ↩
- 2.因為每個消費者都會消費 $z_{1}$ 單位的商品,邊際成本乘上所有消費者的需求量,會是一個固定數。因不論城市怎麼安排、商品從哪裡送,總變動成本加總起來都一樣。舉例來說,舉辦一場活動共有 100 名與會者,每個人需要吃一個 100 元的便當,總成本就是 10,000 元。因此無論叫哪一家便當店做,這 100 個便當的成本就是 10,000 元。如果現在要比較的是「是不是要開兩個取餐點讓大家走近一點?」以及「還是只開一個、但讓大家走遠一點?」,實際上在意的點是交通成本、動線安排這些變動的部分,而不是那 10,000 元便當費,因為那是固定、改變不了的。 ↩
- 3.你可以想像一下,為何便當店總是會寫「超過幾份就提供外送服務」,原因就是如果一次只送一份餐點,油錢 50 元,平均每趟成本就是 50 元。但是如果一次送 10 份,油錢還是 50 元,平均成本變成 5 元。 ↩
- 4.如果某座城市有醫院(假設醫院是高等級商品),那它也一定要有便利商店、診所、文具店(低等級商品)。不可能一個城市有百貨公司但連便利商店都沒有。 ↩